Mathematical modeling links odor-responsive behavior, neural activity, and genes
Summary Text
A research group found that the activity of odor-sensing nerve cells in worms can be expressed by a simple equation and that the more sensitive odor response behavior of worms can be explained by a loss of one "term" of the equation. They have also identified candidate genes involved in "term loss." The study shows that using mathematical models in research can help to better understand brain and nerve function.
Full Text
Humans and animals detect different stimuli such as light, sound, and odor through nerve cells, which then transmit the information to the brain. Nerve cells must be able to adjust to the wide range of stimuli they receive, which can range from very weak to very strong. To do this, they may become more or less sensitive to stimuli (sensitization and habituation), or they may become more sensitive to weaker stimuli and less sensitive to stronger stimuli for better overall responsiveness (gain control). However, the exact way this happens is not yet understood.
To better understand the process of gain control, a research team led by Professor Kimura at Nagoya City University in Japan studied the roundworm C. elegans. They found that, when the worm first smells an unpleasant odor, its nerve cells exhibit a large, quickly increasing, and continuous response to both weak and strong stimuli. However, after exposure to the odor, the response is smaller and slower to weak stimuli but remains large to strong stimuli, similar to the response to the first exposure to the odor. Because the experience of odor exposure causes more efficient movement of worms away from the odor, the nerve cells have changed their response to better adapt to the stimulus using gain control.
Then the researchers used mathematical modeling to understand this process. Mathematical modeling is a powerful tool that can be used to better understand complex biological processes. They found that the "response to first smell" consists of fast and slow components, while the "response after exposure" only consists of the slow component, meaning that the odor experience inhibits the fast component to achieve gain control. They further found that both responses could be described by a simple differential equation and that the slow and fast components correspond to the leaky integration of a first and second derivative term of the odor concentration that the worm senses, respectively. The results of this study showed that the prior odor experience only appears to inhibit the mechanism required for the fast component.
Based on these results, the research team further assumed that the different responses of nerve cells for gain control can be regulated by a relatively simple process involving genes. They then indeed found a set of genes (regulator of G protein and protein kinase G) that are required for the process.
The results of this study represent an insightful use of mathematical modeling to elucidate the basis of nerve cell activity and demonstrate the potential for broadening our understanding of life phenomena by combining mathematical models with various biological experiments.
"The modeling result was totally surprising", said Prof. Kimura. "Because multiple aspects of the nerve cell responses are different, we expected more complicated processes would be involved. The simple model encouraged us to find key genes that change all aspects of the difference, and we think we did it."
In conclusion, this research highlights the importance of mathematical modeling in better understanding complex biological processes. By combining mathematical models with biological experiments, researchers can gain new insights into the way that cells and organisms function and propose new experiments, which may not be possible without modeling. This can ultimately lead to new breakthroughs in the fields of biology and medicine.
A research group found that the activity of odor-sensing nerve cells in worms can be expressed by a simple equation and that the more sensitive odor response behavior of worms can be explained by a loss of one "term" of the equation. They have also identified candidate genes involved in "term loss." The study shows that using mathematical models in research can help to better understand brain and nerve function.
Full Text
Humans and animals detect different stimuli such as light, sound, and odor through nerve cells, which then transmit the information to the brain. Nerve cells must be able to adjust to the wide range of stimuli they receive, which can range from very weak to very strong. To do this, they may become more or less sensitive to stimuli (sensitization and habituation), or they may become more sensitive to weaker stimuli and less sensitive to stronger stimuli for better overall responsiveness (gain control). However, the exact way this happens is not yet understood.
To better understand the process of gain control, a research team led by Professor Kimura at Nagoya City University in Japan studied the roundworm C. elegans. They found that, when the worm first smells an unpleasant odor, its nerve cells exhibit a large, quickly increasing, and continuous response to both weak and strong stimuli. However, after exposure to the odor, the response is smaller and slower to weak stimuli but remains large to strong stimuli, similar to the response to the first exposure to the odor. Because the experience of odor exposure causes more efficient movement of worms away from the odor, the nerve cells have changed their response to better adapt to the stimulus using gain control.
Then the researchers used mathematical modeling to understand this process. Mathematical modeling is a powerful tool that can be used to better understand complex biological processes. They found that the "response to first smell" consists of fast and slow components, while the "response after exposure" only consists of the slow component, meaning that the odor experience inhibits the fast component to achieve gain control. They further found that both responses could be described by a simple differential equation and that the slow and fast components correspond to the leaky integration of a first and second derivative term of the odor concentration that the worm senses, respectively. The results of this study showed that the prior odor experience only appears to inhibit the mechanism required for the fast component.
Based on these results, the research team further assumed that the different responses of nerve cells for gain control can be regulated by a relatively simple process involving genes. They then indeed found a set of genes (regulator of G protein and protein kinase G) that are required for the process.
The results of this study represent an insightful use of mathematical modeling to elucidate the basis of nerve cell activity and demonstrate the potential for broadening our understanding of life phenomena by combining mathematical models with various biological experiments.
"The modeling result was totally surprising", said Prof. Kimura. "Because multiple aspects of the nerve cell responses are different, we expected more complicated processes would be involved. The simple model encouraged us to find key genes that change all aspects of the difference, and we think we did it."
In conclusion, this research highlights the importance of mathematical modeling in better understanding complex biological processes. By combining mathematical models with biological experiments, researchers can gain new insights into the way that cells and organisms function and propose new experiments, which may not be possible without modeling. This can ultimately lead to new breakthroughs in the fields of biology and medicine.
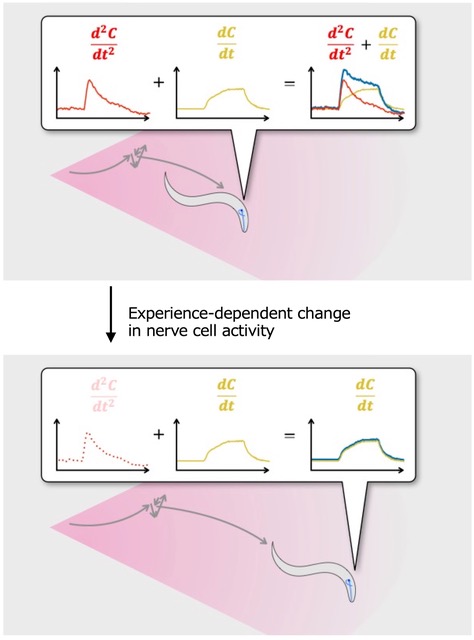
IMAGE: worm and equation
The response to the first smell (blue line in upper panel) comprises of both fast (red line; the second derivative of odor concentration) and slow (yellow line; the first derivative) components. In contrast, the response after exposure-experience (lower panel) only consists of slow components, leading to more efficient movement away from the odor.


